Introduction

In the previous articles, we explored the Binary Tree. Today, we will have a look at Binary Search Trees. Binary Search Tree is a special type of Binary Tree which follow some special properties. The properties are as follows.

1. The left subtree of a node contains only nodes with keys lesser than the node’s key.
2. The right subtree of a node contains only nodes with keys greater than the node’s key.
3. The left and right subtree each must also be a binary search tree.

Time Complexities & Functions in a Binary Search Tree.

We will talk about 2 main things, Insertion and Searching. We know that in a Binary Search Tree, data is stored in a specific manner. So insertion needs to follow that pattern and even in searching we can take advantage of few things.

When inserting a new node in the Binary Search Tree, we have to compare the data and the current node's value. If the data to be inserted is greater, then we go to the right subtree and if smaller, then we go to the left subtree. We do it until we reach the leaf node and add the new node there.

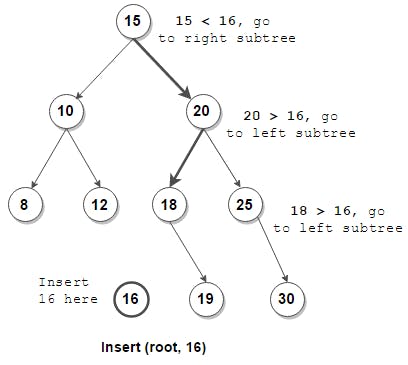
The code for insertion in a Binary Search Tree looks like this. We call our insert function recursively untill we reach the leaf node. The key here is how we are calling the function.

Node* Insert(Node* root, int value)
{
if (!root)
    {
        // Insert the first node, if root is NULL.
        return new BST(value);
    }

    // Insert data.
    if (value > root->data)
    {
        // Insert right node data, if the 'value'
        // to be inserted is greater than 'root' node data.

        // Process right nodes.
        root->right = Insert(root->right, value);
    }
    else
    {
        // Insert left node data, if the 'value'
        // to be inserted is greater than 'root' node data.

        // Process left nodes.
        root->left = Insert(root->left, value);
    }

    // Return 'root' node, after insertion.
    return root;
}

Now, let's talk about searching. This is where a Binary Search Tree is much better than a general Binary Tree. If you remember, for searching an element in the Binary Tree, the worst-case complexity was O(N).

Here, the worst-case complexity is O(Log(N)). We are arranging data in such a fashion that we will never get a skewed tree. Forget about skew, the maximum height of the tree will only be Log(N). N is the number of nodes. Hence, the complexity to search an element in the worst case would be O(Log(N)).

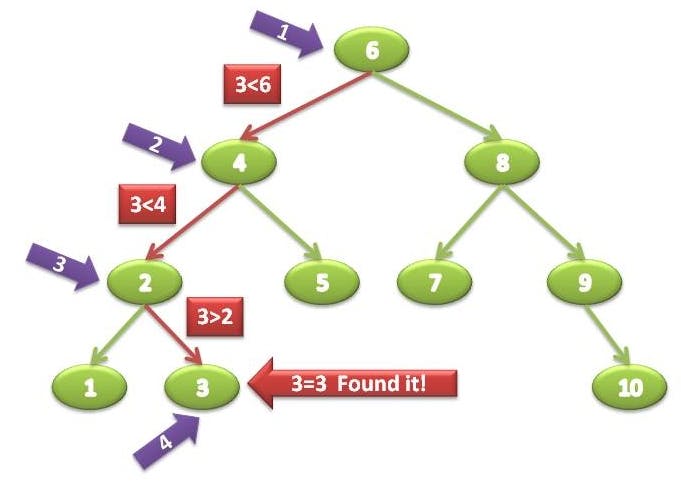
Here is the code for searching in a Binary Search Tree.

struct node* search(struct node* root, int key)
{
    // Base Cases: root is null or key is present at root
    if (root == NULL || root->key == key)
       return root;

    // Key is greater than root's key
    if (root->key < key)
       return search(root->right, key);

    // Key is smaller than root's key
    return search(root->left, key);
}

The image below shows what the code above is trying to do.

Talking about traversals, Binary Search Tree also has the same type of traversals. Pre-order, Post-order, In-order, and Level-order. One special thing is that the inorder traversal of a binary search tree gives us data in a sorted order.

Use-Cases of Binary Search Tree

• They are also helpful to implement various searching algorithms.
• It is helpful in maintaining a sorted stream of data.
• Maps and Sets data structures are internally implemented using self-balancing BSTs
• BSTs are used for indexing and multi-level indexing.

Conclusion

That's it. That was everything you needed to know about Binary Search Trees. There is not much difference between a binary tree and binary search tree but very small difference that makes a binary search tree very useful in some cases.

So this concludes our article series on Binary Trees. We have covered enough for beginner level. Now, you know the time complexities, the functions, syntax, traversals, and difference between Binary Tree and Binary Search Tree.