Introduction

Binary Tree is one of the most important data structures in programming. We have learnt about Arrays, Linked Lists, Stacks, and Queues in my previous articles. All of them are linear data structures but Binary Tree is a hierarchical data structure. Binary Tree is a subdomain of Trees. It is called Binary because it can have at most 2 children.

Just like Linked Lists, we have nodes here too but the arrangement of nodes is not linear. The topmost node is called as root of the tree. In a Binary Tree, every node has two pointers that points to two other nodes. These two nodes are called as children of the node. Here is an example of a binary tree 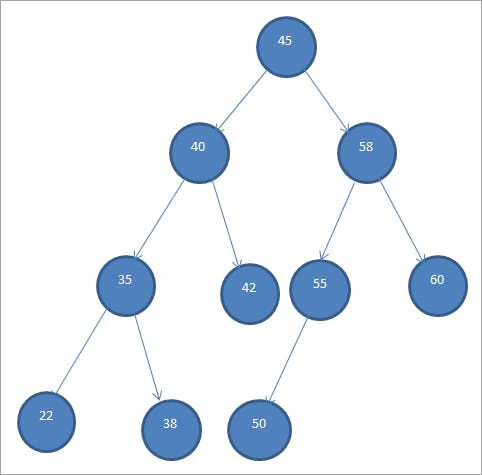Here 45 is the root node of the tree. 40 and 58 are its children. Similarly 35 and 42 are children of 40 and so on...

Basic Syntax and Time Complexities.

Now that you know what is a Binary Tree, let's have a look at how we can create one.

class node
{
    int data;
    struct node* left;
    struct node* right;
};

Looks familiar right? It is the same as a single linked list with one extra pointer. Let's see how we can create a new node.

int main()
{
Node* root = new Node();
root->data = 1;

Node* r1 = new Node();
r1->data = 2;

Node* l1 = new Node();
l1->data = 3;

root->left=l1;    // left child of root is l1 
root->right=r1; // right is r1.
// The tree will look something like this.
                          1
                       /     \
                     3        2
}

That's it. Talking about tree traverals, it won't be possible to cover such an important topic inside the same article. So we will have a look at it in [this article.](cswithiyush.hashnode.dev/a-guide-to-tree-tr..

Things to remember in a Binary Tree

1. Height of the tree can be at max of size N. It is called as a skew tree.
2. Tree Traversals take on an average O(Log(N)) time. N is the number of nodes.
3. The maximum number of nodes at level ‘l’ of a binary tree is 2^l. (Root is l=0).
4. Here are some more points to remember.

Applications of a Binary Tree.

1. Manipulate sorted lists of data.
2. Manipulate hierarchical data.
3. As a workflow for compositing digital images for visual effects.
4. Router algorithms.

Conclusion

So this concludes our article on the basics of binary trees. We have covered what a binary tree is, what are some of its key properties, and its applications. In the next article, we will have a look at the most important part of a Binary Tree i.e different type of tree traversals.