Introduction

In the previous article, we studied about maps and unordered maps. Today, we will have a look at a similar data structure called as set. Like maps, even set has 2 types. Ordered and unordered. Sets are also a part of the STL in C++.

Set in programming is same as a set in real life. It stores unique values in an ordered manner. Let's have a look at the syntax, its in-built functions, time-complexities, and its uses.

Syntax & In-built functions.

This is how you declare a set in C++.

set<int>s1 // set<data_type>[set name].

Insertion, deletion, and searching in set is also a single line code. We can do all three like this.

s1.insert(1); 
s1.find(1);     // gives a boolean
s1.erase(1);

The time complexity of these 3 functions are as follows;

1. Insertion: O(LogN)
2. Searching: O(LogN)
3. Deletion: O(LogN)

Exactly same as an ordered map because even sets are implemented as binary search trees internally. Some other useful functions of a set are

1. count(value) // returns the 1 if value present and 0 if not.
2. size()
3. upper_bound(s.begin(),s.end(),2)
4. lower_bound(s.begin(),s.end(),2)

   Properties of Sets

5. The set stores the elements in sorted order.
6. All the elements in a set have unique values.
7. The value of the element cannot be modified once it is added to the set, though it is possible to remove and then add the modified value of that element. Thus, the values are immutable.
8. Sets follow the Binary search tree implementation.
9. The values in a set are unindexed.

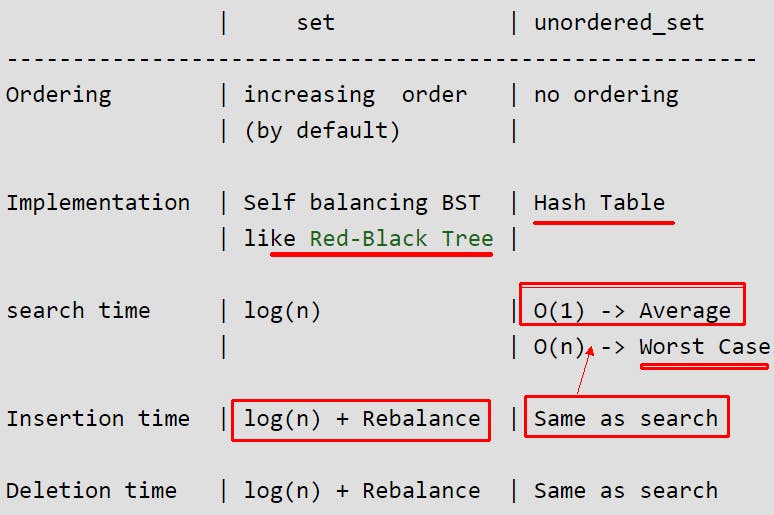
Sets vs Unordered Sets.

Not going to show the syntax of unordered sets because it will just increase the article's length for no reason. All the functions and methods are same for an unordered set except lower_bound() & upper_bound() because data is not sorted in unordered set. The declaration of an unordered set looks like this.

unordered_set<int>s; // unordered_set<data_type> [set name]

The major difference in an ordered set and an unordered set comes in the time complexities. The time complexities for insert,search, and delete in an unordered set are;

1. Insert: O(1), Worst Case: O(N)
2. Search: O(1), Worst Case: O(N)
3. Delete: O(1), Worst Case: O(N)

The reason for the O(N) complexity is once again the concept of collisions in hash tables. If you don't know what is a hash table, then go and read this article where I have explained it in short.

Use sets when

1. you need ordered data.
2. you would have to print/access the data (in sorted order).
3. you need predecessor/successor of elements.

Use unordered sets when

1. You need to keep a set of distinct elements and no ordering is required.
2. You need single element access i.e. no traversal.

Maps vs Sets

The question is when to use map and when to use set. It is simple. If you want to keep count of a particular value in an array, then use map. The key would be the element and the value would be its count.

Suppose you are traversing an array and need to know the elements you have already visited at a particular index, then an unordered_set is the best. It will give you the element in O(1) time.

Conclusion.

Well, this was it. This was pretty much everything you must know about sets and unordered sets as a beginner. We have discussed its syntax, time-complexities, and differences. In the next article, we will cover the basics of graphs. That will probably be the last article of the Data Structure series

Glad to share that my blog is also featured on tech-blogs.dev. A collection of the best tech blogs in the tech community.