Introduction
We have covered all the fundamental Data Structures like arrays, linked lists, strings, and binary trees. Today we will have a look at a data structure called as Maps. which uses these fundamental data structures internally and makes our life easy as a developer.
Map is a part of the Standard Template Library (STL). There are 2 types of maps. Ordered Map & Unordered Map. We will have a look at both of them and understand their differences and similarities. Let's start with ordered maps.
Ordered Maps.
- As the name suggests, ordered map is a data structure where data is stored in an increasing order.
- Ordered maps uses self-balancing binary search trees under the hood. So in that way it stores data in a sorted manner and the time to access, insert, delete is also very efficient.
- Maps store data in the form of key-value pair. The data type of a key can be an integer, boolean, string, double, and float.
- The data type of a value can be anything.
- The keys in the map must be unique. It won't map a single key to two different values.
Basic Syntax & Functions.
This is how you declare an ordered map in C++.
map<int,int>m; map<data_type,data_type> [map name]
You can insert new elements in the map in the following way. Also, if you don't have an element in the map, you can still initialize it with some random value without doing any checks.
m.insert({3,4}); // key is 3 and value is 4.
cout<<m[3]<<endl; // we can access a map element by key
m[3]=m[3]+1; // changes the 4 to 5.
cout<<m[3]<<endl;
We can access an element in the map in 2 ways.
- Using the [] operator.
- Using the iterator/pointer.
- Using the .at() method Let's see how it is done.
// using the [] operator
cout<<m[3]<<endl;
// using the iterator.
auto it = m.begin(); // points to the first element in the map.
cout<<(it->first)<<endl; // gives the key.
cout<<(it->second)<<endl; // gives the value
// using the .at() method.
cout<<m.at(3);
Deleting is fairly simple.
m.erase(3);
There are other in-built functions in maps which are pretty useful like
// gives a true if 3 is present as a key or gives false if not
m.find(3);
// gives an iterator to 5 and if 5 is not present, then to just greater than 5.
m.lower_bound(5);
// gives an iterator to an element just greater than 5.
m.upper_bound(5);
//clears the whole map.
m.clear();
As we discussed above, maps can only store a unique key. What if wanted to use maps but needed more than one occurences of a particular key? Here comes Multimaps.
Multimaps is completely the same as maps, the only difference is that we can map a single key to multiple values.
Time Complexities of an Ordered Map.
- Insertion: O(LogN)
- Search: O(LogN)
- Deletion: O(LogN)
It is the same as a Binary Search Tree.
Unordered Maps.
As the name suggests, these are maps where data is not ordered. In unordered maps, data is stored in form of a hash table. Something like this.
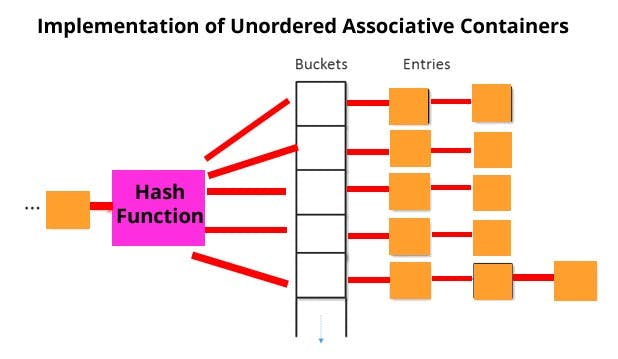 Looks a bit advanced? Let's simplify it.
Looks a bit advanced? Let's simplify it.
- A hash function is a simple or a complex mathematical formula that sets the rule of where our data should go.
- For example if my hash function is x % 100189 where x is my key, then 7 will go to block no 7. All the values that are mapped to key=7, will form a linked list/vector in front of it.
- In real life, the hash function that is used is a bit complex so that there are very less chances of collision. Now what is a collision?
- A collision occurs when two keys are hashed to the same index in a hash table. Collisions are a problem because every slot in a hash table is supposed to store a single element.
- How do we solve this? Not our topic of concern right now. We will cover hashing and hash tables in some other article or you can even Google about it.
- Collision increases the time complexity of all the operations.
- Hence we try to minimize the collision as much as we can using a better hash function or methods like chaining.
So much theory right. This was pretty much everything that you must know as a newbie when it comes to unordered maps. Now moving onto the syntax and basic functions. It is the same as the maps. The only difference is that we use unordered_map instead of a map. Like this:
unordered_map<int,int>m; map<data_type,data_type> [map name]
How do we insert elements? Again the same
m.insert({3,4}); // key is 3 and value is 4.
cout<<m[3]<<endl; // we can access a map element by key
m[3]=m[3]+1; // changes the 4 to 5.
cout<<m[3]<<endl;
Searching is also the same. Talking about in-built functions, you will get the same functionalities as the ordered map except the lower_bound and upper_bound. These two exists only when the data is in sorted manner.
Time Complexities.
Unordered Map generally has better time complexity when compared to an ordered map but due to collisions, the worst-case complexity can be way bad than the ordered maps.
- Insertion: O(1), Worst-Case: O(N)
- Searching: O(1), Worst-Case: O(N)
- Deletion: O(1), Worst-Case: O(N)
The O(1) would look very tempting but use the unordered maps very carefully. The test cases in good coding websites are designed to generate collisions. So you may think that the TC is O(1) but it can go uptill O(N) and give you a Time Limit Error.
If you are completely sure that there are no collisions, or if your keys are some complex data structure like a vector or a 2d vector then go for unordered maps over ordered ones. If you are not sure and have a primitive data type as a key, then ordered maps are generally better because of its O(LogN) complexity in any case.
Conclusion.
So this concludes our guide on the fundamentals of maps. Now, you will be able to tell the difference between maps and unordered maps, how they work internally, what are its time complexities and when to use what.
Go and explore other in-built functions of these two containers and try to solve some basic questions on them.